WebRig
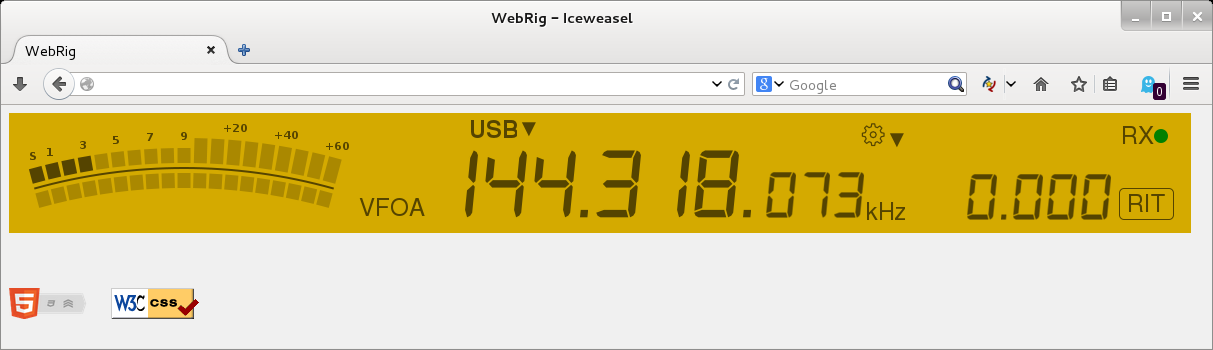
Webrig is web application that allows remote control of hamradio transceiver. It uses today's web technologies like HTML5 and AJAX to provide same experience as desktop application. It does not transfer audio.
Current state is proof of concept.
Contents
Screenshot
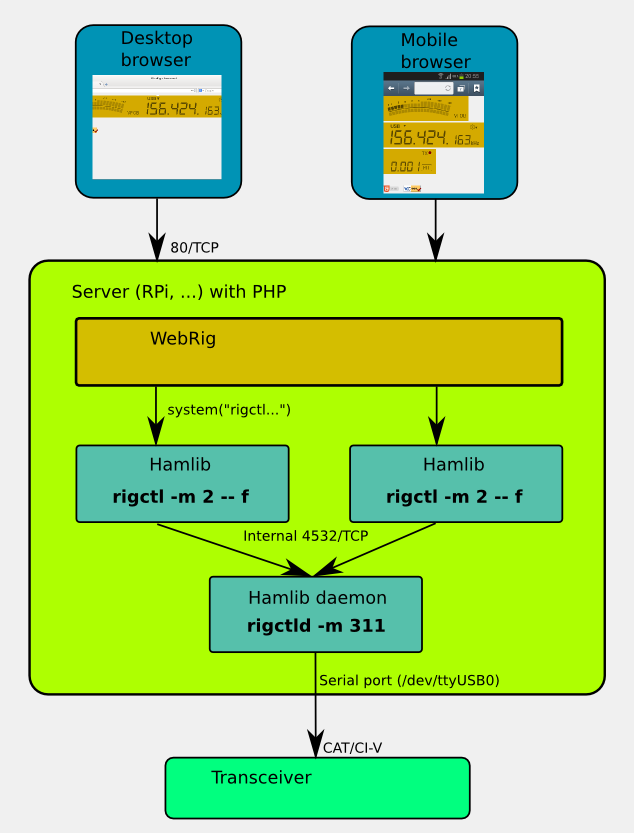
Principles of operation
Webrig consists of some small PHP scripts. It should run on any web server (apache) with PHP support. To access rig (transceiver) it uses hamlib utility rigctl. WebRig is calling rigctl periodically to read rig state like frequency, mode etc. When user changes rig settings, WebRig sends appropriate command to radio. Because of using of rigctld daemon, more users can access the rig simultaneously.
How to install
- Download the archive from http://ok1zia.nagano.cz/webrig/ and unzip they into tree of webserver (maybe /var/www/webrig).
- Install hamlib utilities: sudo apt-get install libhamlib-utils
- Search for model number of your rig: rigctl -l. Next text assume 311.
- Test if hamlib can communicate with radio: rigctl -m 311 -r /dev/ttyUSB0 f. This command should return current frequency. In case of problems try to add -vvvvv command to show verbose informations.
- When you discover proper options, run rigctld: nohup rigctld -m 311 -r /dev/ttyUSB0 &. Ampersand means command is run on background. If you want to stop it, use killall rigctld. Good way is add this command to the end of /etc/init.d/rc.local script (or similar, depends on your distribution).
- Connect to server using web browser.
How to tune
WebRing is supporting more possibilities for QRG and RIT tune.
- Use left and right mouse buttons to click the digit you want to change
- Use mouse wheel to change then digit
- On touch devices, touch and hold the digit you want to change. Move finger up or down to change the digit.
Options
- Refresh - how often you want to refresh rig state
- Low orders - what happen to lower order digits when you tune. Possibilities are Keep and Clear.
- VFO set - if use VFO's A+B or Main+Sub
Authors
- OK1ZIA - idea, code
- OK1HRA - graphics design, βtesting
Wish list
- A=B
- Server unavailable information