Difference between revisions of "Contest"
(→Upload live score to slovhf.net) |
(→Upload live score to slovhf.net) |
||
| Line 44: | Line 44: | ||
==Upload live score to [http://slovhf.net/en/claimed/ slovhf.net]== | ==Upload live score to [http://slovhf.net/en/claimed/ slovhf.net]== | ||
| − | Upload current score once to slovhf.net. You have to register on this web and enter your user name in [[Setup#Contest_defaults|Contest defaults]] dialog. | + | Upload current score once to slovhf.net. You have to register on this web and enter your user name in [[Setup#Contest_defaults|Contest defaults]] dialog. Note account create takes some days to proceed. |
==Upload to [http://vhfcontest.net/ vhfcontest.net]== | ==Upload to [http://vhfcontest.net/ vhfcontest.net]== | ||
Latest revision as of 15:29, 17 October 2017
Contents
- 1 No contest opened
- 2 Contest opened
- 2.1 Save
- 2.2 Fill operators
- 2.3 QSO Check
- 2.4 Export as EDI
- 2.5 Upload live score to slovhf.net
- 2.6 Upload to vhfcontest.net
- 2.7 Export as report
- 2.8 Export as ADIF
- 2.9 Export as HTML
- 2.10 Export Statistics
- 2.11 Export title page
- 2.12 Export as Cabrillo
- 2.13 Export as MediaWiki
- 2.14 Upload to MediaWiki
- 3 About imports
No contest opened
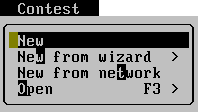
New
Opens new contest. Pre-filled values are default for standard IARU VHF Contest. Dialog is decribed in Contest options.
New from wizard
Opens menu where you can choose pre-fill contest options for know types of contest. After it, Tucnak shows Contest options dialog so you can make changes.
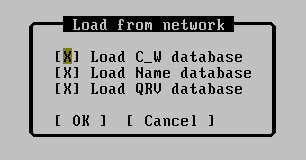
New from network
Shows context menu with all stations on the network. You can choose one. Dialog will show:
Choose databases which you want to load to the local PC. In case of large databases and slow connection is good idea to skip some.
Open
Opens existing contest. Program lists all contests in your directory, you can choose one of them.
Contest opened
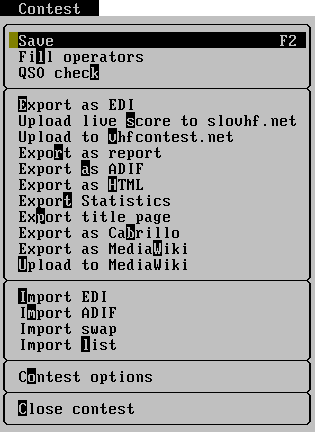
Save
Save all changes to disk. It is normally not needed to use because Tucnak saves data after each QSOo (Autosave). Some minor changes saved into contest files does not force automatic save so it's good to press F2 manually.
Fill operators
Settings of all bands have a list of operators (items Mope1 and Mope2 EDI format). Each list contains callsigns of all operators which have one or more QSO. This feature is suitable used before you send logs to contest commitee.
First run of Export as EDI also runs this function.
QSO Check
This function uses all available informations to find errors in your log. It checks same things as QSO Info. It shows question mark next to suspicious call. The > flag means QRB is above average. If you have no better thing to do, you can also check these QSOs to save points.
Warning: it takes some seconds to complete. On slow PC's it should seem to tucnak freeze.
Export as EDI
EDI is standard exchange format for Region 1. If operators field is not filled, fills it.
Upload live score to slovhf.net
Upload current score once to slovhf.net. You have to register on this web and enter your user name in Contest defaults dialog. Note account create takes some days to proceed.
Upload to vhfcontest.net
Export as report
Report is legacy format used in OK Activity contest before internet epoch.
Export as ADIF
ADIF is standard file for QSO exchange for non-contest purposes. For example general logs, LOTW or EQSL.CC.
Export as HTML
This function exports all QSOs into tables in HTML format. You can simply upload it on your web pages. Bands reference to images snapBN.png, preferred way is to take snapshot of map (F1), to fix file names and upload images with HTML.
Export Statistics
Export contents statistics window into text file f.e. to upload it to web.
Export title page
Title page is also legacy format, probably used once by me.
Export as Cabrillo
Cabrillo is used mostly for ARRL contest robots. This support is experimental, please check it in text editor, fill all unfilled values and check if contains all informations of contest report. Be aware I don't run these contest so I depend on informations from users, that can be incomplete.
Export as MediaWiki
Export report of contest in [www.mediawiki.org MediaWiki] format. Useful as template for web article about the contest.
Upload to MediaWiki
About imports
You can import only into opened contest because import file formats have insufficient infomations (scoring, information about your station...). Functions show inputline, you must enter file name here.
Import EDI
For import from other VHF logs. For Taclog look at Converting TACLog v 1,9xx C_W files for use with Tucnak
Import ADIF
Tested with exports from:
- EI5DI, V14.22
- N1MM
Import swap
Service function to recover SWP files created by Tucnak in case of loss of TXT files.
Import list
Not for contests. Import text file with list of stations (not QSOs). Useful for locator visualisation (list of beacons, packet nodes, repeaters...). Format of file is:
CALL WWL REMARK
Remark is optional.
Contest options
Opens Contest options dialog where you can modify contest options.
Close contest
Closes contest, you can open other contest or create new.